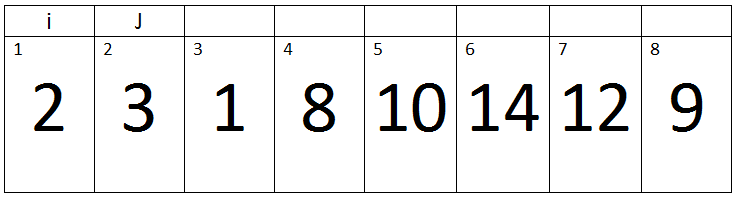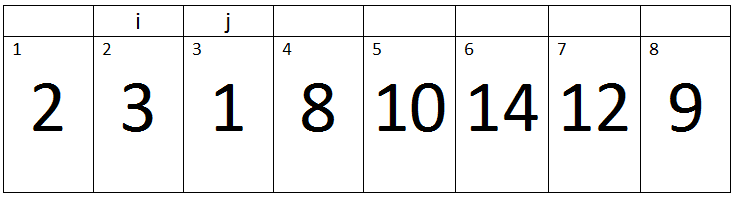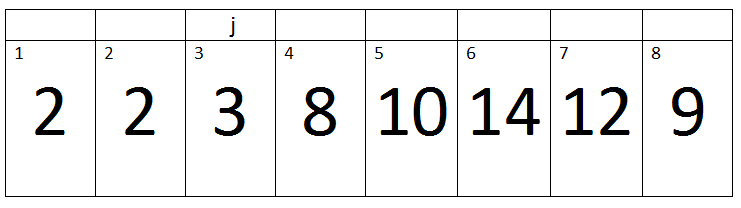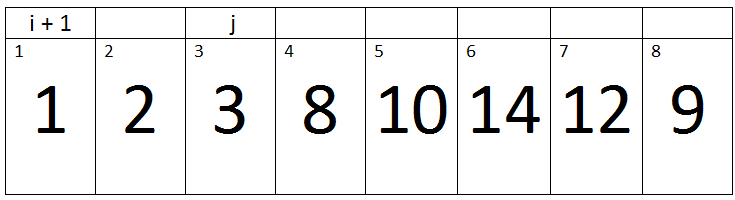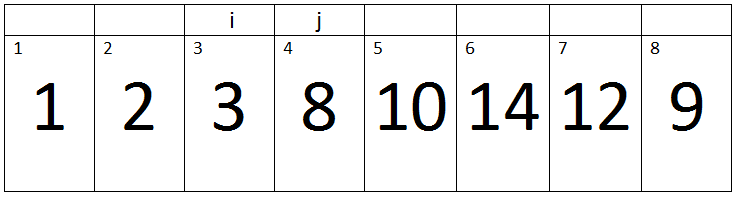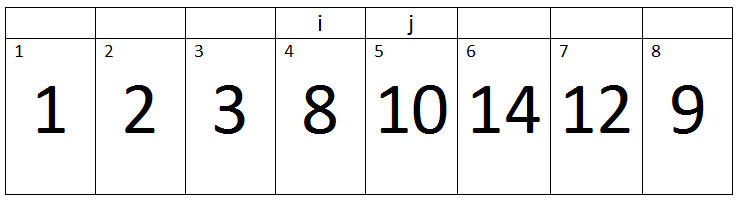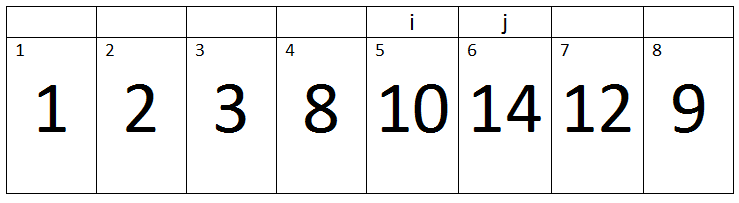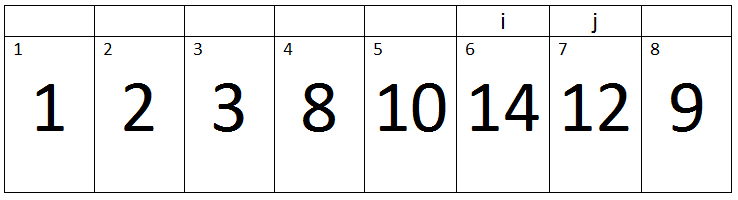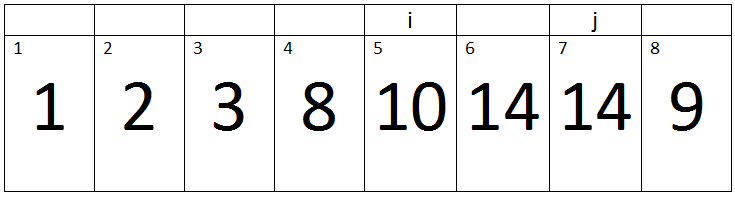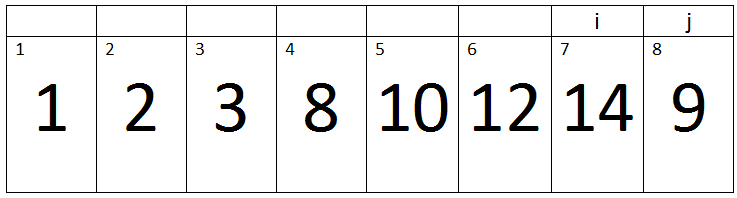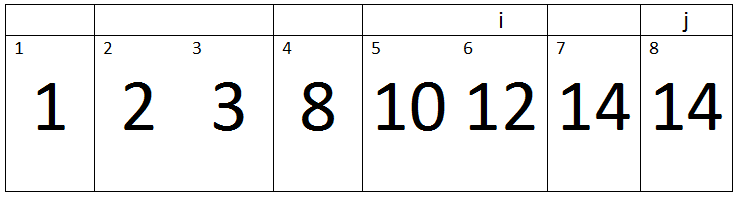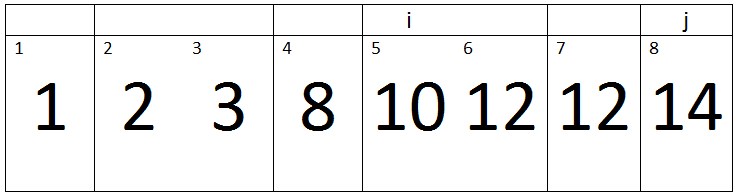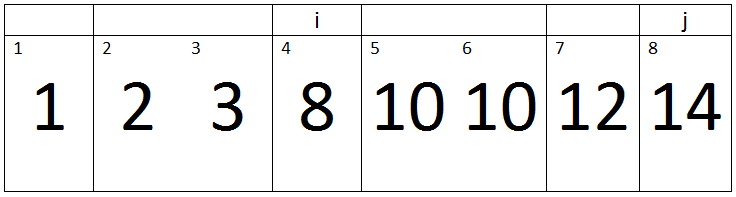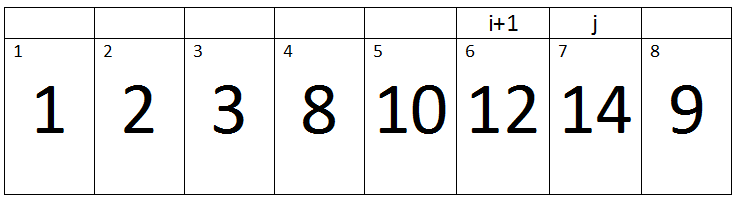
Insertion sort C++ is one of the most commonly used algorithm in C++ language for the sorting of fewer values or smaller arrays. It is preferred our Selection sort but other faster algorithms like bubble sort, QuickSort, and Merge Sort are preferred our insertion sort. The Insertion sorting C++ is implemented by the use of nested loops, it works in a way such that the key will be placed in a properly sorted sequence. In this tutorial, we will discuss the working of C++ insertion sort algorithm with proper examples so that you can understand it easily. At the end of this tutorial, we will also discuss its running time. Now let’s see towards the algorithm of insertion sort in C++.
Insertion Sort Algorithm:-
Insertion-Sort(A[]) For (j=2 to A.length) Key = A[j] // Insert A[j] into the sorted sequence A[1…… j-1] i=j – 1 ---- While(i >= 0 and A[i] > key) ------- A[i + 1] = A[i] ------- i = i – 1 A[i + 1] = key
Example of Insertion Sort C++ Implementation:-
#include<iostream>
#include<conio.h>
using namespace std;
main()
{
int Key;
int array[8];
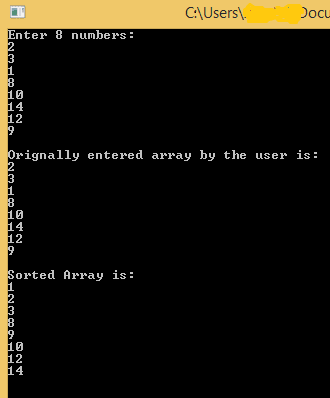
cout<<"Enter 8 numbers: "<<endl;
for(int i=0; i<8; i++)
{
cin>>array[i];
}
cout<<endl;
cout<<"Orignally entered array by the user is: "<<endl;
for(int j=0; j<8; j++)
{
cout<<array[j];
cout<<endl;
}
cout<<endl;
for(int j=1 ; j < 8 ; j++)
{ Key = array[j];
int i = j-1;
while(i >= 0 && array[i] > Key)
{
array[i + 1] = array[i];
i = i - 1;
}
array[i + 1] = Key;
}
cout<<"Sorted Array is: "<<endl;
for(int i=0; i<8; i++)
{
cout<<array[i]<<endl;
}
getch();
}
Explanation of C++ Insertion Sort Algorithm:-
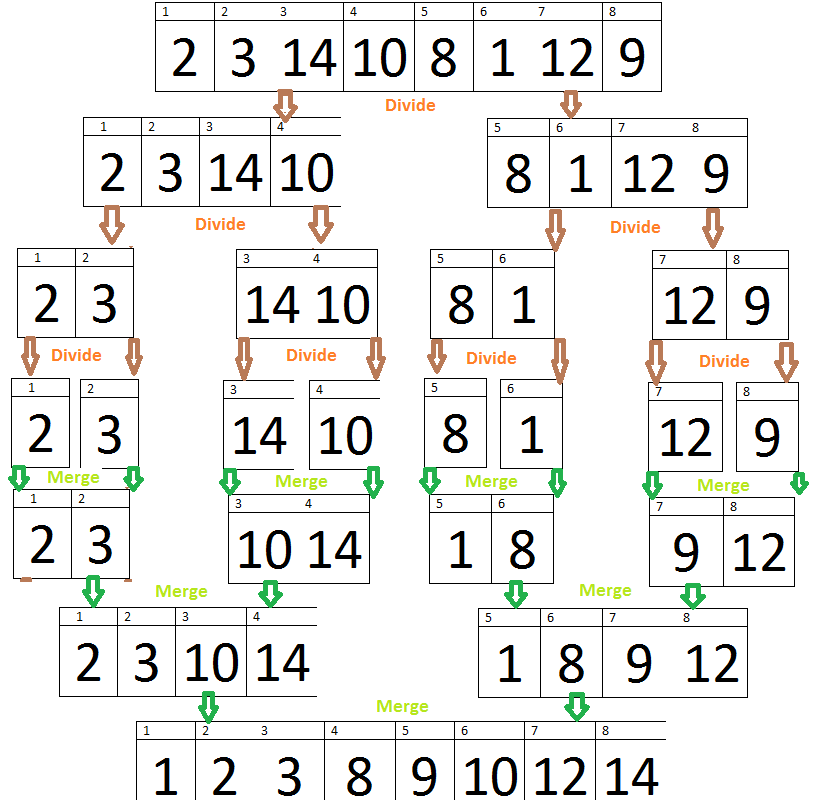
Above I have provided insertion sort C++ code and now we will take an example array of eight elements and we will apply insertion sorting C++ on it, we will discuss its working with complete steps and explain it with detailed explanations and images. Let A = {2, 3, 1, 8, 10, 14, 12, 9} be an array of eight elements. As you can see in the above algorithm, the array ‘A’ will be passed to the function Insertion-Sort. First of all, control will be transferred to the outer loop. In this tutorial, the “Pass” keyword will represent the iterations of an Outer loop.
First Pass:-
(j < A.length) -> True
Here j=2, key= 3, i= 1.
Now inner loop will begin.
Iteration 1:-
i > 0 and A[i] > key -> 1>0 and 2 > 3 -> condition false. Therefore loop will terminate and the value of key will be assigned to A[i + 1]. In short there will be no change in our array.
Second Pass:-
(j < A.length) -> True
Here j=3, Key=1, and i=2.
Iteration 1:-
i > 0 and A[i] > key -> 2>0 and 3 > 1 -> True.
Therefore A[i + 1] assigned a[i].
‘i’ will be decremented, So its value becomes 1.
Iteration 2:-
Here j=3, Key=1 and i=1.
i > 0 and A[i] > key -> 1>0 and 2 > 1 -> True.
Therefore A[i + 1] assigned a[i].
‘i’ will be decremented, So its value becomes 0.
Iteration 3:-
Here j=3, Key=1 and i=0.
i > 0 and A[i] > key -> 0>0 and 0 > 1 -> False.
Therefore, the loop will terminate.
After the termination of a loop, the value of key will be assigned to A[i+1].
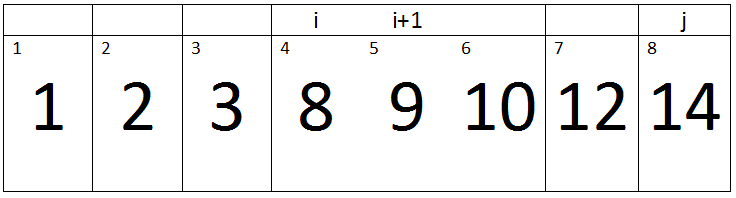
Third Pass:-
(j < A.length) -> True
Here j=4, Key=8, and i=3.
Iteration 1:-
i > 0 and A[i] > key -> 3>0 and 3 > 8 -> False.
Therefore, a loop will terminate and the value of key will be assigned to A[i + 1]. So there will be no change in our array.
Fourth Pass:-
(j < A.length) -> True
Here j=5, Key=10, and i=4.
Iteration 1:-
i > 0 and A[i] > key -> 4 > 0 and 8 > 10 -> false.
Therefore, a loop will terminate and the value of key will be assigned to A[i + 1]. It means our array will remains same.
Fifth Pass:-
(j < A.length) -> True
Here j=6, Key=14, and i=5.
Iteration 1:-
i > 0 and A[i] > key -> 5 > 0 and 10 > 14 -> false.
Therefore, a loop will terminate and the value of key will be assigned to A[i + 1]. So no change in our array.
Sixth Pass:-
(j < A.length) -> True
Here j=7, Key=12, and i=6.
Iteration 1:-
i > 0 and A[i] > key -> 6 > 0 and 14 > 12 -> True.
Therefore A[i + 1] assigned a[i].
‘i’ will be decremented, So its value becomes 5.
Iteration 2:-
Here j=7, Key=12 and i=5.
i > 0 and A[i] > key -> 5>0 and 10 > 12 -> False.
Therefore, a loop will terminate and the value of key will be assigned to A[i + 1].
Seventh Pass:-
(j < A.length) -> True
Here j=8, Key=9, and i=7.
Iteration 1:-
i > 0 and A[i] > key -> 7 > 0 and 14 > 9 -> True.
Therefore A[i + 1] assigned a[i].
‘i’ will be decremented, So its value becomes 6.
Iteration 2:-
Here j=8, Key=9 and i=6.
i > 0 and A[i] > key -> 6 > 0 and 12 > 9 -> True.
Therefore A[i + 1] assigned a[i].
‘i’ will be decremented, So its value becomes 5.
Iteration 3:-
Here j=8, Key=9 and i=5.
i > 0 and A[i] > key -> 5 > 0 and 10 > 9 -> True.
Therefore A[i + 1] assigned a[i].
‘i’ will be decremented, So its value becomes 4.
Iteration 4:-
Here j=8, Key=9 and i=4.
i > 0 and A[i] > key -> 4 > 0 and 8 > 9 -> False.
Therefore, a loop will terminate and the value of key will be assigned to A[i + 1].
Eighth Pass:-
Here (j= 9),
(j < A.length) -> False
Therefore, the condition will become false, Outer loop will be terminated and we will get a sorted array at the end of this insertion sort C++ code.
Running Time of Insertion Sort:-
Worst Case:-
Insertion Sorts C++ worst case will occur when given array is in descending order because if an array is present in descending order then the inner loop will run maximum times. Worst case is -> n2.
Average Case:-
If given array does not contain elements in ascending order and it also doesn’t contain elements in descending order. Then inner will run at least once, Therefore average running time is also n2.
Best Case:-
If given array contains elements is ascending order then the inner loop will not run even for once, therefore, the running time will be n.
If you have any questions regarding insertion sorting in C++ then post them on our forum or in a comment section of this post.