Binary Search:-
The flaw of a binary search is that it could only be applied on a sorted array. We cannot apply it on an unsorted array. This is a very useful technique because it is used to quickly found the required values. This technique is performed is several steps.
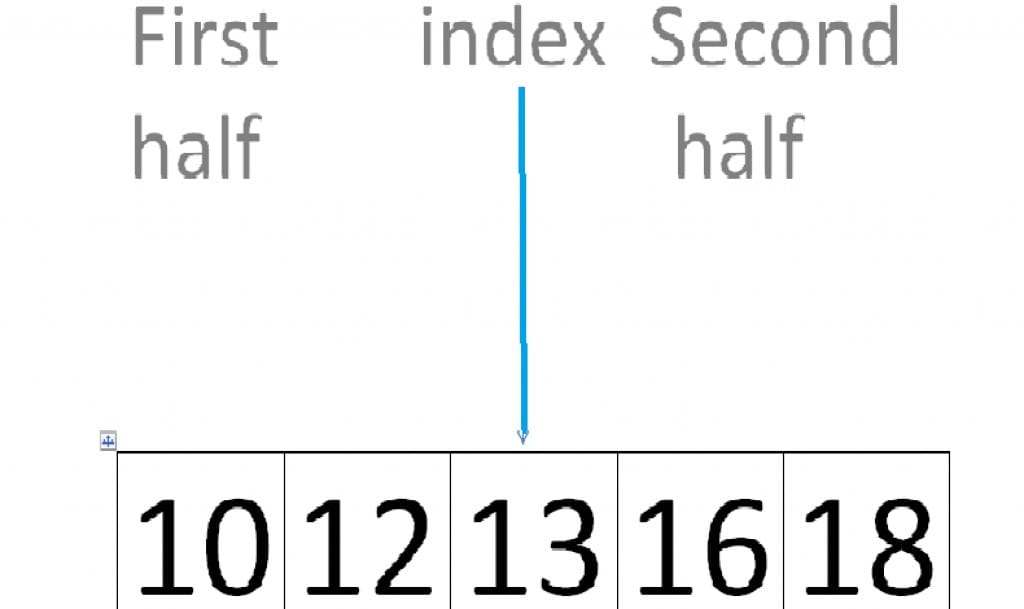
1. Firstly the middle element of array is found and compared with value which user wanted to search in an array.
2. If they are same then it will return the location of the required value.
3. If they are not equal then it will break the array in half.
4. If the middle element of array is smaller than the required number then it will search the first half of an array.
5. If the middle element of array is greater than the required number then it will search the second half of an array.
This process will continue until the required value is found or until the loop terminates or complete without founding the required value.
Example of Binary Search:-
#include<iostream.h>
#include<conio.h>
main()
{
int abb[4];
int r;
int initial=0;
int final=4;
int mid;
int location=-5;
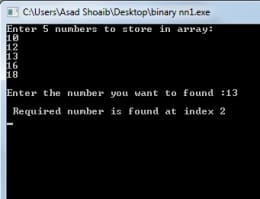
cout<<"Enter 5 numbers to store in array: "<<endl;
for(int i=0; i<5; i++)
{
cin>>abb[i];
}
cout<<endl;
cout<<"Enter the number you want to found :";
cin>>r;
cout<<endl;
while(initial<=final)
{
mid= (initial+final)/2;
if(abb[mid]==r)
{
location=mid;
break;
}
if(r<abb[mid])
final=mid-1;
if(r>abb[mid])
initial=mid+1;
}
if(location==-5)
cout<<" Required number not found "<<endl;
else
cout<<" Required number is found at index "<<location<<endl;
getch();
}
Explanation:-
The above program is written to take five values as an input from the user and store them in an array named abb. Then the program will ask the user about which number he wanted to search, then user will provide the element to be searched. First of all array abb willbe declared then integer variable r will be declared to hold the required value and the elements input by the user will be assign to array abb. Integer variable initial will be declared to hold the position of first index of an array then the integer variable final will be declared to the location of the last element of an array, Then the integer variable mid will be declared to hold the location of the middle element of the array. After declaring variables the values assigned to an array by using for loop, number to be searched will be assigned to variable r. Then, while loop will come into action and the conditioned will be processed, the loop will continue until initial index remains smaller than the final index. If the condition becomes true it will add the initial and final index and divide them by two and store the resultant value in a variable mid. Then it will check the other condition, if mid equals to the required number then it will assign the value of mid to the variable location, otherwise it will check either the required number is smaller than the number present at the mid location, if it is smaller than it will assign variable final the value of mid-1. If it is greater than it will assign variable initial the value of mid+1. At the end when the loop completes, the compiler checks the value of variable location, if it is equal to -5, it will print the massage “value not found” otherwise it will return the location of a required number.
Program of Prime numbers:-
The below program will show how to develop and design the logic of prime numbers.
#include<iostream>
#include<conio.h>
using namespace std;
bool prime(int);
main()
{
int a;
cout<<"Enter an interger greater then 1: ";
cin>>a;
if(prime(a))
cout<<a<< " is a prime Number "<< endl;
else
cout<<a<<" is not a prime Number";
getch();
}
bool prime(int z)
{
for(int i=2; i<z; i++)
{
if(z%i==0)
return false;
}
return true;
}
[yop_poll id=”14″]
If you like my article on Binary search in C++ and wanted to read my other articles then visit my Homepage.
@ 2014 HellGeeks.com