Searching in Arrays:-
The process of finding the required data in an array is called searching. It is very useful when the size of an array is very large.
Normally, there are two types of searching techniques used in C++.
1. Sequential search.
2. Binary search.
Sequential Search:-
Sequential search in C++ is also called a linear search. This searching technique is very simple, to perform this technique the user starts the loop from the zero index of an array to the last index of an array. It starts from the first index and compared the required value with the first value.
If the required value is found it will show the result otherwise compare the value of next index and it will continue until the required value is found or loop completes without finding any value.
Example of Sequential Search:-
#include<iostream.h>
#include<conio.h>
main()
{
int arr1[5];
int req;
int location=-5;
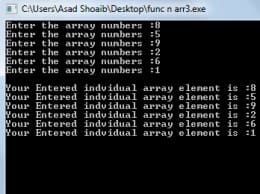
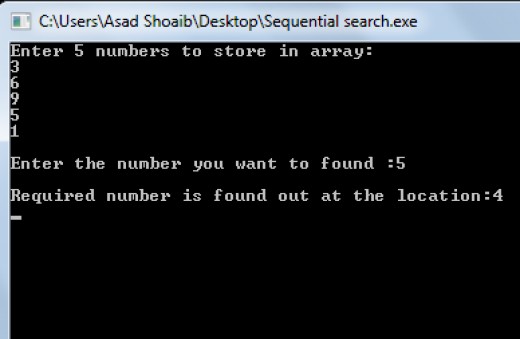
cout<<"Enter 5 numbers to store in array: "<<endl;
for(int i=0; i<5; i++)
{
cin>>arr1[i];
}
cout<<endl;
cout<<"Enter the number you want to find :";
cin>>req;
cout<<endl;
for(int w=0;w<5;w++)
{
if(arr1[w] == req)
location=w;
}
if(location !=-5)
{
cout<<"Required number is found out at the location:"<<location+1;
cout<<endl;
}
else
cout<<"Number is not found ";
getch();
}
Explanation:-
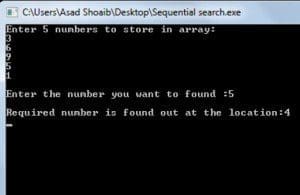The above program will declare an integer array named arr1 to assign the values input by the user. Then it will declare variable req to assign the value of a required number, it will declare variable location to store the location of the required value. The program uses only one for loop to search the number, the loop will run from the zero index to the last index of an array. Therefore, it will compare the element at the index zero with the number user wanted to search. If both numbers are same then it will assign the value of the loop variable to the location variable. If they does not match then it will compare the value of required number with the next index, the process will continue until the value found or loop completes without finding anything.
Code for Prime Numbers:-
Following code is developed for the beginners, which is designed by a simple logic which anyone could understand easily.
#include<iostream.h>
#include<conio.h>
void fprime(int);
main()
{
int i, j;
cout<<"Enter the number: ";
cin>>j;
fprime(j);
getch();
}
void fprime(int a)
{
int ans=0;
for(int i=2; i<a; i++)
{
if (a%i==0)
{
ans=1;
break;
}
}
if(ans==1)
{
cout<<a<<" is not a Prime Number "<<endl;
}
else
cout<<a<<" is a Prime Number "<<endl;
}
Explanation:-
Following program will take an input from the user and store it into the variable ‘j’. Then it will call the function fprime, which will apply the logic on the given number and show that either the number is the prime number or not a prime number. The simple logic behind the function is that it will run the loop from 2 to the input number minus 1. IF the loop number modulus given number is zero then it will not a prime number else it is a prime number.
Code for the Program of Magic Numbers:-
Magic numbers are those numbers whose sum of the digits is equal to 1.
Example:-
100 is a magic number because when we take a sum of its digits it will be equal to 1.
i.e
1+0+0=1
Following code is developed to evaluate either the given number is the magic number or not the magic number. This code for the program of magic numbers is developed for the beginners.
#include<iostream.h>
#include<conio.h>
class magic{
private :
int q1,q2,q3,w1;
int a,d,e;
public:
void mymagic()
{
cout<<"Enter a 3 digit number :"<<endl;
cin>>a;
w1=a;
q1=a%10;
a=a/10;
q2=a%10;
a=a/10;
q3=a;
d=(q1+q2+q3);
e=d;
cout<<endl;
if(d==10)
{
cout<<w1<<" is a magic number"<<endl;
}
else if(d%10==0)
{
div();
}
else
{
cout<<w1<<" is not magic number"<<endl;
}
}
void div()
{
if(d%10==0)
d=d/10;
{
if(d==10)
{
cout<<w1<<" is a magic number :";
}
else
{
div();
}
}
}
};
main()
{
magic m;
m.mymagic();
getch();
}
[yop_poll id=”13″] If you like my work and wanted to read my other articles then visit my Homepage.
@ 2014 HellGeeks.com
